摘要:介绍IIR数字滤波器的传统设计思想与步骤。及其计算机辅助设计方法。以一数字带通滤波器为例,着重说明了基于MATLAB的三种实现手段:模拟低通原型、合适模拟带通及直接原型,为数字滤波器设计带来全新的实现手段,设计快捷方便,仿真波形直观。
数字滤波器是具有一定传输选择特性的数字信号处理装置,其输入、输出均为数字信号,实质上是一个由有限精度算法实现的线性时不变离散系统。它的基本工作原理是利用离散系统特性对系统输入信号进行加工和变换,改变输入序列的频谱或信号波形,让有用频率的信号分量通过,抑制无用的信号分量输出。数字滤波器和模拟滤波器有着相同的滤波概念,根据其频率响应特性可分为低通、高通、带通、带阻等类型,与模拟滤波器相比,数字滤波器除了具有数字信号处理的固有优点外,还有滤波精度高(与系统字长有关)、稳定性好(仅运行在0与l两个电平状态)、灵活性强等优点。数字滤波器按单位脉冲响应的性质可分为无限长单位脉冲响应滤波器IIR和有限长单位脉冲响应滤波器(FIR)两种。本文介绍(IIR)数字滤波器的设计与分析。
1 IIR数字滤波器设计思路与步骤
IIR 数字滤波器可用一个n阶差分方程
y(n)=Σbrx(n-r)+Σaky(n-k),
或用它的Z域系统函数:
对照模拟滤波器的传递函数:
不难看出,数字滤波器与模拟滤波器的设计思路相仿,其设计实质也是寻找一组系数{b,a},去逼近所要求的频率响应,使其在性能上满足预定的技术要求;不同的是模拟滤波器的设计是在S平面上用数学逼近法去寻找近似的所需特性H(S),而数字滤波器则是在Z平面寻找合适的H(z)。IIR数字滤波器的单位响应是无限长的,而模拟滤波器一般都具有无限长的单位脉冲响应,因此与模拟滤波器相匹配。由于模拟滤波器的设计在理论上已十分成熟,因此数字滤波器设计的关键是将H(S)→H(Z),即,利用复值映射将模拟滤波器离散化。已经证明,冲击响应不变法和双线性变换法能较好地担当此任,则在此基础上,数字滤波器的设计就可首先归结为模拟滤波器的设计了。
数字滤波器的设计步骤如图1所示。
图1 数字滤波器设计步骤
2 IIR数字滤波器设计方法
IIR数字滤波器的设计方法有多种,可归纳为下述两种。
2.1 传统设计方法
根据前述设计思路,首先设计一个模拟原型滤波器(截止频率为1rad/s的低通滤波器),然后在模拟域(S平面)进行频率变换,将模拟原形滤波器转换成所需类型(指定截止频率的低通、高通、带通、带阻)的模拟滤波器,再将其数字离散化,从S平面映射至Z平面,得到所需技术指标的数字滤波器。
上述过程中,也可先将模拟原型离散化,得到数字原型滤波器,继而在数字域(Z平面)进行频率变换,得到所需类型的数字滤波器。
模拟滤波器到数字滤波器的转换可在时域进行也可在频域实现,时域转换的关键是要使数字滤波器与模拟滤波器时域响应的采样值相等,以保持其瞬态特性不变,常用的是冲击响应不变法。频域变换法必须使得数字滤波器在-π≤ω≤π范围内的幅频特性与模拟滤波器在-π/T≤Ω≤π/T 范围内的幅频特性一致,即保证S平面与z平面上幅频特性的一一单值对应关系,常用的是双线性变换法。
2.2 计算机辅助设计方法
传统设计方法思路清晰,步骤详尽,可参阅公式、手册循章而行。但由于计算繁琐,手工计算大多只能用来进行简单低阶选频滤波器(如LP,HP,BP及BS等)的设计。计算机辅助设计方法是集电路理论、网络图论、数值分析、矩阵运算、元件建模、优化技术、高级计算机语言等多交叉学科于一身的新领域,它把计算机的快速、高精度、大存储容量、严格的逻辑判断和优良的数据处理能力与人的思维创造能力充分结合起来,极大地简化了数字滤波器的设计过程。在优秀科技应用软件MATLAB的信号处理工具箱中,提供了一整套模拟、数字滤波器的设计命令和运算函数,方便准确,简单易行,使得设计人员除了可按上述传统设计步骤快速地进行较复杂高阶选频滤波器的计算、分析外,还可通过原型变换法直接进行各种典型数字滤波器设计,即应用MATLAB设计工具从模拟原型直接变换成满足原定频域指标要求的数字滤波器。
此外,MATLAB软件还提供了强大的数字滤波器优化设计功能。即预先确定一种最佳设计准则,然后直接求得在该准则下滤波器系统的传递函数{b,a}。这种最优设计方法可方便地用于任意幅频特性要求的多带通复杂滤波器系统的设计。
3 各种设计方法的MATLAB实现
下面以一带通数字滤波器的设计为例,说明基于MATLAB的三种实现方法。
3.1 基于模拟低通原型的MATLAB实现
%通过模拟低通原型滤波器进行数字带通设计程序:
fp=480 %模拟低通通带上限频率
fs=520 %模拟低通阻带下限频率
wp=2*pi*fp %模拟低通通带上限角频率
ws=2*pi*fs %模拟低通阻带下限角频率
rp=3 %通带波动
rs=20 %阻带衰减
%巴特沃斯模拟低通原型滤波器设计
[n,wn]=buttord(wp,WS,rp ,rs,'s')
[z,p,k]=buttap(n) %模拟低通原型零、极点系数
[b1,a1]=zp2tf(z,p,k) %零、极点系数转换为传递函数
%巴特沃斯模拟低通原型滤波器频率响应
[hl,w1]=freqs(b1,a1)
mag1=abs(h1)
%模拟低通原型滤波器幅频特性曲线
subplot(221);semilogx(w1,mag1)
fw=40 %模拟带通滤波器带宽频率
bw=2*pi*fw %模拟带通滤波器带宽角频率
% 由模拟低通原型变换为模拟带通滤波器
[b2,a2]=lp2bp(b1,a1,wn,bw) %模拟带通滤波函数系数
%巴特沃斯模拟带通滤波器频率响应
[h2,w2]= freqs(b2,a2)
mag2 =abs(1l2)
%模拟带通滤波器幅频特性曲线(db)
subplot(222);plot(20*log10(mag2))
% 冲击响应不变法进行离散化设计
fo=2000 %采样频率
[bz,az]=impinvar(b2,a2,2000) %数字带通滤波函数系数
%巴特沃斯型数字带通滤波器频率响应
[hz,w]= freqz(bz,az)
magz=abs(hz)
phz=unwrap(angle(hz))
subplot(223);plot(magz) %数字带通滤波器幅频特性曲线
subplot(224);flot(plot) %数字带通滤波器相频特性曲线
3.2 基于合适类型模拟滤波器的MATLAB实现
%通过合适类型模拟滤波器进行数字带通设计程序
fp= [480,520];fs=[450,550] %模拟通带、阻带频率
wp=[480,520]*pi*2 %模拟通带角频率
ws=[450,550]*pi*2 %模拟阻带角频率
rp=3;rs=20 %通带波动、阻带衰减
% 巴特沃斯型模拟带通滤波器设计
[n,wn]=buttord (wp,ws,rp,rs,'s')
[b,a]=butter(n,wn,'s') %模拟带通滤波函数系数
%巴特沃斯型模拟带通滤波器频率响应
[ha,w]= freqs(b,a)
ma=abs(ha);pha=unwrap(angle(ha))
subplot(421);plot(w/(2*pi),ma) %模拟幅频曲线
subplot(423);plot(w/(2 pi),pha) %模拟相频曲线
% 冲击响应不变法进行离散化设计
fo=5000 %采样频率
[bn,an]=impinvar(b,a,5000) %数字带通滤波函数系数
%巴特沃斯型数字带通滤波器频率响应
[hz,w]=freqz(bn,an)
mz=abs(hz);phz=unwrap(angle(hz))
subplot(422);plot(w,mz) %数字滤波器幅频曲线
subplot(424);plot(w,phz) %数字滤波器相频曲线
hi=impz(bn,an) %数字滤波器冲击响应
subplot(425),plot(hi) %冲击响应曲线
n=0:300;t=n/fo
xl=2*square(2*pi*500*t) %500Hz方波信号
subplot(426);plot(x1) %500Hz方波波形
yi=conv(hi,x1) %时域卷积输出
subplot(427);plot(yi) %卷积输出波形
y1=filter(bn,an,x1) %数字滤波函数输出
subplot(428);plot(y1) %数字滤波器输出波形
3.3 基于直接原型变换法的MATLAB实现
%数字带通滤波器直接设计程序
fp= [480,520];fs=[450,550] %模拟通带、阻带频率
rp=3;rs=20 %通带波动、阻带衰减
fo=10000 %采样频率
%频率指标变换
wp=2*pi*fp/f0 %数字通带频率
ws=2*pi*fs/fo %数字阻带频率
%切比雪夫1型数字带通滤波器直接设计
[n,wn]=cbeblord(wp/pi,ws/pi,rp,rs)
[b,a]=chebyl(n,rp,wn) %数字带通滤波器系数
%切比雪夫1型数字带通滤波器频率响应
[h,w]= freqz(b,a,128,10000)
mag=abs(h;pha=unwrqp(angle(h))
subplot(321);plot(w,mag) %幅频曲线
subplot(322);plot(w,pha) %相频曲线
hi=impz(b,a) %冲击响应
subplot(324);plot(hi) %响应曲线
n=0:500;t=n/fc
x1=2*square(2*pi*500*t) %500Hz方波信号
subplot(323);plot(t,x1) %500Hz方波波形
yi=conv(hi,x1) %时域卷积输出
subplot(326);plot(yi) %卷积输出波形
y1=filter(b,a,x1) %数字滤波函数输出
subplot(325); stem(y1) %数字滤波器输出波形
4 结束语
基于MATLAB的信号处理工具箱为数字滤波器设计带来了全新的实现手段,设计快捷方便,仿真波形直观。上述三种设计方案均可实现设计指标,但以直接原型变换法最为简便。实际应用中,数字滤波器也可以对连续时间信号进行处理,但需要先对连续信号进行A/D变换,经数字滤波后,再经D/A转换得到所需要的连续信号(此处略)。
参考文献
1 倪养华,等.数字信号处理与实现.上海:上海交通大学出版社,1998
2 施阳.等.MATLAB语言工具箱.西安:西北工业大学出版社,1999
-
一款高温报警电路2024年11月13日 81
-
可燃气体全自动点火器2012年09月22日 76
-
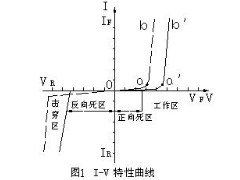
LED参数与特性2012年09月18日 118
-
RC振荡电路的几种接法2012年09月10日 221
-
MAX764极性反转电路2012年08月24日 47
-
实用恒流充电器2012年08月18日 175
-
电子催眠器制作2012年08月15日 72
-
多普勒自动电子开关2012年08月02日 78
-
常用物质金属非金属的电阻率、导电率明细表2024年11月23日 4874
-
自制微型交流电焊机2012年07月14日 1143
-
声光控延时开关的制作2024年07月06日 915
-
用LM1875替找TDA20302012年09月15日 777
-
6N3+LM4780功放制作2012年09月13日 653
-
小型太阳能供电板的制作2012年09月08日 649
-
简单的逆变器电路2012年07月08日 560
-
1000米晶体稳频FM立体声发射机2012年07月22日 499