由于现场可编程门阵列(FPGA)器件具有工作速度快、集成度高和现场可编程等特点,因而在数字信号处理中得到广泛的应用,越来越受到硬件电路设计师们的青睐。直接数字频率合成技术是从相位概念出发直接合成所需波形的一种新的频率合成技术,该技术具有频率分辨率高、频率变换速度快、相位可连续线性变化等特点,在数字通信系统中已被广泛采用。本文基于DDS 的基本原理,利用Altera公司的FPGA芯片ACEX1K系列器件完成了一个DDS系统的设计,设计工具为Altera公司的Quartus设计软件。
1.DDS 的基本原理
DDS 的基本原理是以数控振荡器的方式,产生频率、相位可控制的正弦波。电路一般由N bit 相位累加器、ROM只读存储器(正弦查找表)、数模转换器(DAC)、低通平滑滤波器(LPF)构成,图1 所示为DDS 的基本结构。
图1 中,fc为时钟频率,K为频率控制字,N 为相位累加器的字长,M 为ROM地址线位数,L 为ROM数据线宽度,fO为输出频率。相位累加器由全加器和累加寄存器级联组成。在时钟频率fc的控制下,对输入频率控制字K进行累加,累加满量时就产生溢出。相位累加器的输出对应于该时刻合成周期信号的相位,并且这个相位是周期性的,在0~2π范围内变化。相位累加器位数为N,最大输出为2N-1,对应于2 π的相位,累加一次就输出一个相应的相位码,通过查表得到正弦信号的幅度,然后经过D/A转换器转换为模拟信号,由低通滤波器滤除杂散波和谐波以后,输出一个频率为fo的正弦波。输出频率fo由fC和K共同决定,即fo=fc× K/2N 且K<2N-1。从而,DDS 的最小分辨率△fmin可达△fmin=fc/2N。理论上通过设定DDS相位累加器的位数N、频率控制字K和时钟频率fc的值,就可以产生任一频率的输出。
2.DDS 的FPGA(ACEX EP1K100)实现
ACEX 1K 器件是Altera公司着眼于通信、音频处理及类似场合的应用而推出的芯片系列,总的来看,它将逐步取代FLEX 10K系列,成为首选的中规模器件产品,该芯片主要有以下优点:
- 高性能。 ACEX 1K器件采用查找表(LUT)和EAB(嵌入式阵列块)相结合的结构,特别适用于实现复杂逻辑功能和存储器功能。
- 高密度。典型门数为1万到10万门,有多达49152位的RAM(每个EAB 有4096 位RAM)。
- 系统性能。 器件内核采用2.5V电压,功耗低,能够提供高达250MHz的双向输入输出功能,完全支持33MHz 和66MHz 的PCI 局部总线标准。
- 灵活的内部互连。具有快速连续式延时可预测的快速通道互连。
本设计采用的是ACEX EP1K100器件,DDS 的FPGA 实现框图如图2 所示。其中,输入端K2 为频率控制字,决定了DDS的频率分辨率,K1 为初相控制字,CLK为时钟频率,EN为使能引脚,RESET为复位引脚,SIN为输出的正弦离散序列。在用FPGA设计DDS 电路的时候,相
位累加器是决定DDS 性能的一个关键部分。因此,为了提高系统的工作速度,在设计DDS 的累加寄存器模块和全加器模块时并没有采用FPGA 单元库中的16~32 位加法器,尽管它们可以很容易地实现高达32位的相位累加器,但是当工作频率较高时,这种方法有较大的延时,不能满足速度的要求。因此,具体实现时采用了4个4位的累加器以流水线的方式实现16 位累加器。仿真结果表明,采用流水线技术可以大大提高系统的工作速度。
用FPGA 设计DDS 电路的另一个关键是相位/幅度转换电路。设计中面临的主要问题是资源的开销。电路通常采用ROM 结构,通过取相位累加器的高若干位为ROM 的地址输入,经查表(LUT)和运算后,ROM 就输出所需波形的量化数据。ROM 一般在FPGA 中由EAB 实现,且
ROM 表的尺寸随着地址位数或数据位数的增加呈指数递增关系。因此,在满足信号性能的前提下,应该尽可能地减少资源的开销。实际设计时,我们充分利用了正弦信号周期内的对称性和算术运算来减少EAB 的开销。
模块ROM 8 × 1 6 为被调用的LPM_ROM 元件, 利用它可在ACEX 1K器件的内部ROM 中存放一张28 × 16 位的正弦表。通过在ROM 表中存储四分之一周期的量化幅度值,采用适当的地址变换,就可以表示正弦信号整个周期的量化幅度值,这样就节省了将近四分之三的资源。
由于LPM_ROM只加载*.mif或*.hex类型的文件。用MATLAB 产生类型为*.mif或*.hex正文格式的正弦表,加上文件头和文件尾,即可存为类型为*.mif或*.hex 的文件,从而加载到LPM_ROM中,完成DDS 的相位/ 幅度转换。
现在令CLK的周期为10ns,初相K1=0,频率控制字K2分别为80和160,通过Quartus软件进行仿真,各数据的时序关系如图3 所示。
仿真结果生成*.pof文件后,经过D/A转换和低通滤波器,即可在示波器上看到所得的正弦波形,如图4 所示。
3.DDS 的杂波分析
由图4可知,所得的正弦波有很多毛刺,这主要是由相位舍位误差、幅度量化误差和D/A抽样等因素产生的杂波造成。
实际的DDS 系统,一般只取相位累加器输出的高M 位来寻址ROM,而把(N-M)位舍去,这就引入了相位舍位误差。经过理论分析,当取fc=100MHz,N=16,M =10,则频率控制字K 取64的整数倍时,没有相位舍位误差,输出频率范围为0.01~50MHz。
任意一个幅度值要用无限长的比特流才能精确地表示,而实际上ROM 查询表的输出位数L 是个有限值,这就会产生幅度量化误差。设正弦波的幅度值用L 位二进制码表示,则幅度量化的信噪比随着量化位数L 的增加而提高。本设计中,L = 16,幅度量化的信噪比可达98.08dB。
由D/A 抽样产生的杂波可以用低通滤波器滤除。
-
热敏电阻温度阻值查询程序2024年11月13日 74
-
C99语法规则2024年11月16日 675
-
FreeRTOS 动态内存管理2024年11月12日 448
-
一款常用buffer程序2024年11月06日 88
-
1602液晶显示模块的应用2012年08月03日 192
-
GNU C 9条扩展语法2024年11月18日 261
-
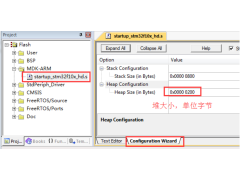
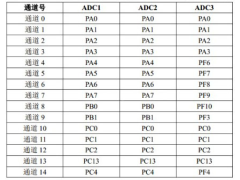
如何实现STM32F407单片机的ADC转换2024年11月15日 300
-
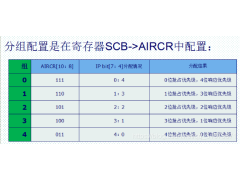
STM32使用中断屏蔽寄存器BASEPRI保护临界段2024年11月15日 195
-
C99语法规则2024年11月16日 675
-
51单片机LED16*16点阵滚动显示2012年09月05日 664
-
FreeRTOS 动态内存管理2024年11月12日 448
-
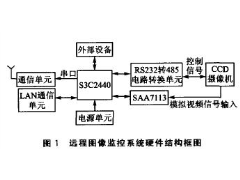
ARM9远程图像无线监控系统2012年07月03日 424
-
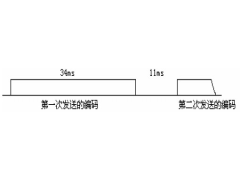
用单片机模拟2272软件解码2012年09月06日 300
-
如何实现STM32F407单片机的ADC转换2024年11月15日 300
-
新颖的单片机LED钟2012年08月06日 278
-
GNU C 9条扩展语法2024年11月18日 261